KNN —— 基本介绍与简要实现
本文共 1346 字,大约阅读时间需要 4 分钟。
KNN
介绍
knn又叫做k最近邻,也是一个分类的算法,其基本思想如下:
我们预测一个样本属于哪一类,就看在一定范围内,它离那个类别最近。
K代表你指定的范围,比如你指定K为7,就是说在离测试数据最近的7个样本中,哪个类别占得多,那我们就把测试数据分到那一类。
一般来说如果是二分类的话,K都会取奇数,免得出现一样的情况。
步骤
- 计算测试点到所有样本点的距离
- 对距离进行从小到大排序
- 取前K个最近的距离,找到对应的类别
- 那个类别最多就把测试点归到哪一类
实现
sklearn中自带了一些数据集,这里以鸢尾花为例;
数据包括四个特征: 花萼长度、花萼宽度、花瓣长度、花瓣宽度 ;
类别有三个:山鸢尾花、变色鸢尾花、维吉尼亚鸢尾花。用0、1、2表示;
K取5。
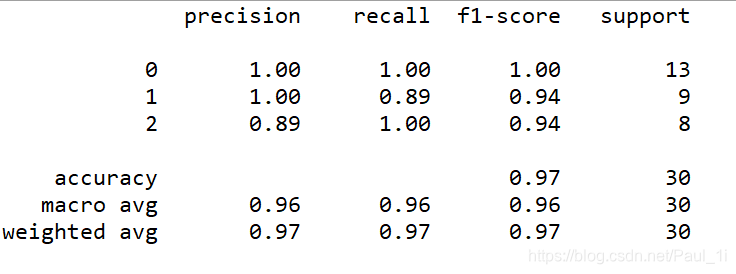
import numpy as npfrom sklearn import datasetsfrom sklearn.model_selection._split import train_test_splitfrom sklearn.metrics import classification_reportdef knn(x_test,x_train,y_train,k): x_data_size = x_train.shape[0] # 求距离 diffMat = np.tile(x_test,(x_data_size,1))-x_train dis = (diffMat**2).sum(axis=1) dis = dis**0.5 # 排序,argsort排序存的是索引,不是值 sortedDis = np.argsort(dis) # 统计前k个最近点的标签 classCount = { } for i in range(k): label = y_train[sortedDis[i]] classCount[label] = classCount.get(label, 0)+1 sortedClassCount = sorted(classCount.items(), key=lambda item:item[1], reverse=True) return sortedClassCount[0][0]# 导入sklearn自带的鸢尾花数据集iris = datasets.load_iris()# 切分测试机,训练集x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,test_size=0.2)# knn环节predictions = []for i in range(x_test.shape[0]): predictions.append(knn(x_test[i], x_train, y_train, 5))# 计算指标print(classification_report(y_test,predictions)) 以上例子计算得出的正确率、召回率和F1如下图所示:
转载地址:http://hehe.baihongyu.com/
你可能感兴趣的文章